Question

Write the center radius and the equation of the circle in standard from shown on the graph

Answer 1

`x^2+(y+2)^2=8^2`

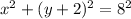
Step-by-step explanation:

We apply the equation of circle instandard form:

`\begin{gathered} (x-h)^2+(y-k)^2=r^2 \\ \text{where the center of circle = (h, k)} \\ r\text{ = radius} \end{gathered}`

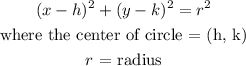
We need to determine the center of circle from the graph given:

From the graph, the center is at 2 units below the origin (0, 0) on the y axis.

This coordinate corresponds to (0, -2)

The center (h, k) = (0, -2)

h = 0 and k = -2

The radius is the distance from the center of the circle to the circumference.

The distance is 8 units

radius = 8 units

Inserting the formula into the equation:

`\begin{gathered} (x-0)^2+(y-(-2))^2=8^2 \\ x^2+(y+2)^2=8^2\text{ or} \\ x^2+(y+2)^2=\text{ 64} \end{gathered}`