Question

The sum of two numbers is 134. If three times the smaller number is subtracted from the larger number, the result is 18. Find the two numbers.The larger number isThe smaller number is

Answer 1

Let, larger number be x and smaller number be y.

Condition 1: The summ of two numbers is 134.

It can be written as,

`x+y=134\ldots\ldots\text{.}(1)`

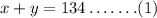
Condition 2: If three times the smaller number is subtracted from the larger number, the result is 18.

The equation is,

`x-3y=18\ldots\ldots\ldots\text{.}\mathrm{}(2)`

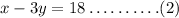
Solving equation 1 and 2,

`\begin{gathered} \text{subtract equation (2) from (1),} \\ x+y-(x-3y)=134-18 \\ x+y-x+3y=116 \\ 4y=116 \\ y=29 \end{gathered}`

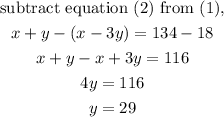
Out the value of y=29 in equation (1),

`\begin{gathered} x+y=134 \\ x+29=134 \\ x=105 \end{gathered}`

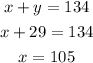
Answer:

Larger number is x=105

Smaller number is y=29.