To solve this problem, we will use the following fact about circles. Given the circle
whenever we are given two tangent lines, the angle formed between then (in our picture angle theta or angle ABC) is related to the intercepted arcs as follows
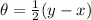
where y and x are measured in degrees.
For our particular problem, we have the following
So, using the fact that we introduced at the beginning, we have the following equation
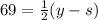
However, note that since arcs y and s form the whole circle, this means that their measure (in degrees) should add up to the measure of the whole circle (360°). So we have the following equation
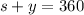
So, we can subtract s on both sides to get
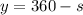
Now, we replace this value of y in our first equation, so we get

Note that arc s is the one described by the central angle x. So, this means that
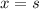
So if we replace this in our equation, we get
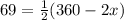
If we multiply both sides by 2, we get
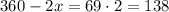
Now, we can add 2x on both sides, so we get
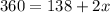
Then, we subtract 138 on both sides, so we get

Now, we divide both sides by 2. So we get
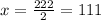
So the value of x is 111°