Given:
a = 13
b = 16.9
A = 26 degrees
Asked: What are the values for angles B and C and side c?
Solution:
To solve this problem, we will be needing the formula for the sine law.
Sine Law Formula:
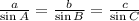
Now, we will first solve for the angle B.
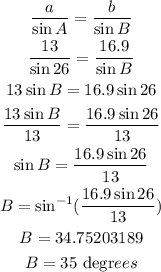
Now that we have angle B, we can now find angle C by combining all the angles and equate it to 180 degrees.
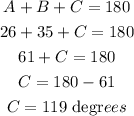
In order to find side c, we will use again the sine law formula.
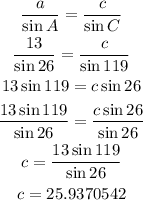
ANSWER:
Angle B = 35 degrees
Angle C = 119 degrees
Side c = 25.9