Question

A 10.0 L flask contains 3.20 g of O2 and an unknown amount of N2. The temperature is 300 K and the total pressure in the flask is 0.739 atm. How many grams of N2 are in the flask?

Answer 1

There are 5.57g of N2 in the flask.

Step-by-step explanation:

1st) With the formula of Ideal gases, and the values of volumen (10.0L), temperature (300K) and the grams of O2, we can convert the grams to moles and calculate the pressure of O2 at those conditions:

`\begin{gathered} \text{ Grams of O}_2\text{ to moles \lparen using the molar mass\rparen:} \\ 3.20g*(1mol)/(32g)=0.1mol \end{gathered}`

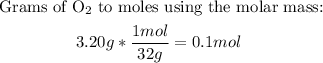
Now we can replace the values in the ideal gas formula:

`\begin{gathered} P_(O2)*V=n_(O2)*R*T \\ P_(O2)*10.0L=0.1mol*0.082(atm*L)/(mol*K)*300K \\ P_(O2)=(2.46atm*L)/(10.0L) \\ P_(O2)=0.25atm \end{gathered}`

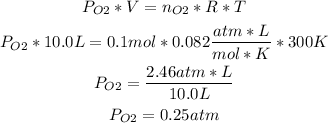
Now we know that the pressure of oxygen gas in the flask is 0.25atm.

2nd) Subtracting the total pressure of the flask minus the pressure of the oxygen, we can calculate the pressure of the nitrogen gas:

`\begin{gathered} P_(total)=P_(O2)+P_(N2) \\ 0.739atm=0.25atm+P_(N2) \\ 0.739atm-0.25atm=P_(N2) \\ 0.489atm=P_(N2) \end{gathered}`

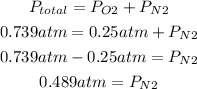
3rd) Finally, with the pressure of nitrogen and the values of volume and temperature, we can calculate the moles of N2 in the flask:

`\begin{gathered} P_(N2)*V=n_(N2)*R*T \\ 0.489atm*10.0L=n_(N2)*0.082(atm*L)/(mol*K)*300K \\ 4.89atm*L=n_(N2)*24.6(atm*L)/(mol) \\ (4.89atm*L)/(24.6(atm*L)/(mol))=n_(N2) \\ 0.199mol=n_(N2) \end{gathered}`

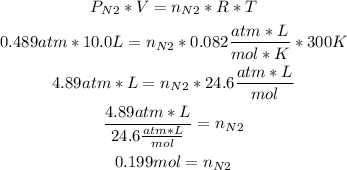
4th) With the molar mass of nitrogen, we can convert the moles to grams:

`0.199mol*(28g)/(1mol)=5.57g`

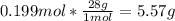
So, there are 5.57g of N2 in the flask.