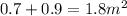Question

2 m² of soil containing 35% sand was mixed into 6 mº of soil containing 15% sand. What is the sand content of the mixture?

Answer 1

In this problem we can calculate the sand amound in each of the elements of the mixture.

1) for the first one: 2m^2 with 35% of sand:

`\begin{gathered} 2\to100 \\ x\to35 \end{gathered}`

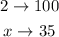
solving the rule of 3 is going to be:

`x=(2*35)/(100)=0.7m^2`

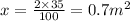
so in the first element we have 0.7 m^2 of sand

2) For the seconf: 6m^2 with the 15% of sand:

`\begin{gathered} 6\to100 \\ x\to15 \end{gathered}`

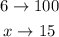
Solving the rule of 3 is going to be:

`x=(6*15)/(100)=0.9m^2\text{ }`

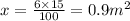
so in the second element we have 0.9 m^2 of sand

So in total the content of sand is:

`0.7+0.9=1.8m^2`