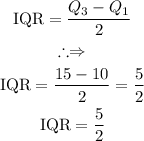Question

Average Life Expectancy Animal Years Bison 15 Cow 15 Deer 8 Donkey 12 EIK 15 Goat 8 Horse 20 Moose 12 Pig 10 Sheep 12 5) Find the median 6) State the 5-number summary: Min, Q1, median, Q3, max values 7) What is the IQR?

Answer 1

Step-by-step explanation: Provided the Data, we need to simply find the (5) (6) and (7):

(5) Median:

Median is simply a middle number or a number that is at the center of the data organized in the order of least to greatest, therefore organizing the data results in the following sequence:

`8,8,10,12,12,12,15,15,15,20`

Median is the middle number if it is odd-numbered or the average of the two middle numbers in the case of the even-numbered data sequence, the median is as follows:

`M=(12+12)/(2)=12`

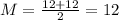
(6) 5-number summary:

(i) Min Is the least number in the data sequence, therefore it is:

`8`

(ii) Q1 or First Quartile, is simply the median of the first half of the data, therefore it is:

`Q_1=10`

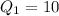
(iii) Median It has been calculated already in the (5) part of this question, therefore it is:

`12`

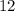
(iv) Q3 Third Quartile, is simply the median of the second half of the data, and likewise, it is:

`15`

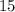
(v) Max value

`20`

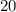
(7) IQR

The interquartile range has the following simple formula:

`\begin{gathered} \text{IQR}=(Q_3-Q_1)/(2) \\ \end{gathered}`

Therefore the interquartile range is as follows:

`\begin{gathered} \text{IQR}=(Q_3-Q_1)/(2) \\ \therefore\Rightarrow \\ \text{IQR}=(15-10)/(2)=(5)/(2) \\ \text{IQR}=(5)/(2) \end{gathered}`