We need to complete the perfect square. A perfect square has the following form:
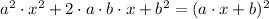
In our case we have:
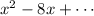
We can immediately deterine the value of "a", which is the root of number multiplying x², since this number is 1, then:
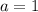
This also means we can find "b", because the second term is equal to the product of 2, a, and b. So we have:
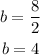
With this we can determine the blank, because it is b². So we have:
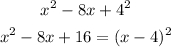
The first missing space is 16 and the second is 4.