We need to solve the system:
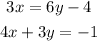
The first step is to isolate one of the variables and replace it at the other equation. We will isolate the "x" variable on the first equation:
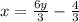
Then we replace this value on the second equation:
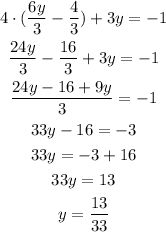
We can use this value to determine x.
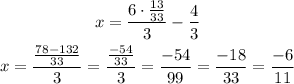
The solution to the system is (-6/11, 13/33)