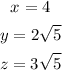Pythagorean theorem:
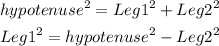
Use the pythagorean theorem above to find the values of x, y and z as follow:
1. From the triangle in the right find the value of y^2 (Leg 1)
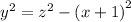
2. From the triangle in the left find the value of y^2 (Leg 1):
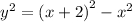
3. From the big triangle find the value of z^2 (Leg 1):
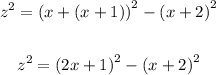
3. Equal the expressions of y^2 (step 1 and step 2):
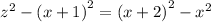
4. Substitute the z^2 in the equation above by the value of z^2 you get in step 3:
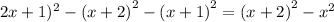
5. Solve x in the equation above:

Use quadratic formula to solve x:
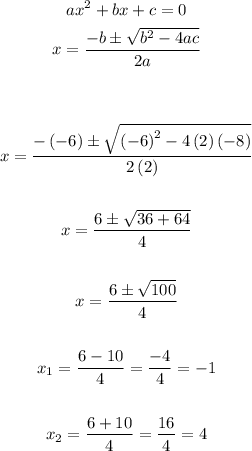
As x cannot be a negative value (a side of a triangle cannot be negative) the value of x is 4
6. Use the value of x to solve y in the equation in step 2:
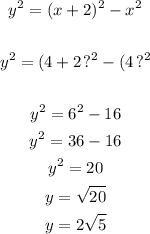
7. Use the value of x to solve z in the equation in step 3:
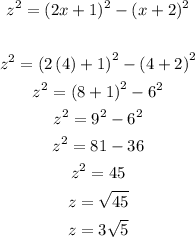
Then, the values of x, y and z are: