Given: Two right triangles are given such that-
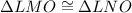
Required: To determine the missing information to prove the given statement.
Explanation: The HL theorem states that two right triangles are congruent if their hypotenuse and a leg of one triangle are equal to the hypotenuse and a leg of another triangle.
We are given two right triangles whose hypotenuse is their common side.
Hence hypotenuse of both triangles LMO and LNO are equal to each other i.e.,
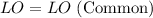
Now we need one leg of both triangles which are congruent to each other.
As there are two legs in both triangles which can be used to prove the congruency-
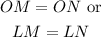
Any one of the legs shown above can be used to prove the congruency of the triangles by HL theoe