ANSWER
The final pressure of the gas is 1350.22 mmHg
Explanation:
Given information

From the question provided, you were asked to find the final pressure of the gas, hence, we assume that x represents the final pressure of the gas
To find the final pressure of the gas, we need to apply the general gas law
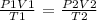
Where,
P1 = initial pressure
V1 = initial volume
T1 = initial temperature
P2 = final pressure
V2 = final volume
T2 = final temperature
The next process is to convert the final and initial temperature from degree Celcius to degree kelvin
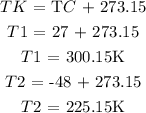
The next thing is to substitute the given data into the above formula

Therefore, the final pressure of the gas is 1350.22 mmHg