Given: A arrangement of the letter 'PATTERNS' is given.
Required: To determine the number of paths that spell the word 'PATTERNS' if all paths must start at the top and move diagonally through the
letters.
Explanation: The Pascal Triangle can be used to determine the number of ways the word 'PATTERNS' can be spelled.
The Pascal Triangle is shown below
One exciting thing about Pascal's Triangle is if we move diagonally from top to bottom, each number denotes the number of ways to get to the position from the top.
Hence to spell the word 'PATTERNS', we would need to get to the 8th row.
Hence we need to add all the entries of the 8th row to get the total number of ways to spell the word.
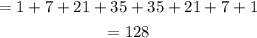
Final Answer: The total number of paths that spells the word 'PATTERNS' is 128.