Let's start by calculating the probability of each event.
Event 1: Since spinner B has 9 red slices and 15 total slices, then the probability of landing in a red slice is:
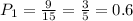
Event 2: Since spinner A has only blue and red slices, it will always land on a blue or a red slice, so the probability is 100%, or 1:
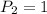
Event 3: Spinne A has 5 blue slices and 10 total slices, so the probability of landing on a blue one is:
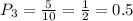
Event 4: Spinner B has 6 blue slices and 15 total slices, so the probability of landing in a blue slice is:
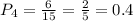
So, from least likely to most likely, we have:
Event 4, Event 3, Event 1, Event 2.