Solve for y intercept and graph -2x + 2y = 8

Question

asked Aug 2, 2023 109k views

1 Answer

Infinito · Answer 1 · 2023-08-07T10:13:39+0000

Solution:

Given the equation below

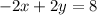
Converting to slope-intercept form of an equation of a straight line

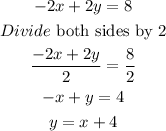
$\begin{gathered} -2x+2y=8 \\ Divide\text{ both sides by 2} \\ (-2x+2y)/(2)=(8)/(2) \\ -x+y=4 \\ y=x+4 \end{gathered}$

Where

The general form of a slope-intercept form of a line is

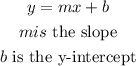
$\begin{gathered} y=mx+b \\ mis\text{ the slope} \\ b\text{ is the y-intercept} \end{gathered}$

Hence, the y-intercept, b, of the line is 4

Using a graphing tool, the graph of the equation is shown below