Question

1Which of the following statements is true?A.A>>{<1OB.0012 A 100 NIH INܝܙܐ ܬܝܳ ܬ݂ܕܣܳ ܚܙܐ܂OC.D.7.3

Answer 1

Verify each statement

A 2/5 > 1/2

Multiply in cross

2*2 > 5*2

4 > 10 -----> is not true

B 1/2 < 2/11

Multiply in cross

1*11 < 2*2

11 < 4 ---> is not true

C 3/4 < 4/5

3*5 < 4*4

15 < 16 ----> is true

D 7/8 < 3/4

7*4 < 8*3

28 < 24 ---> is not true

therefore

The answer is option C

Step-by-step explanation

If you have

`\begin{gathered} (a)/(b)=(c)/(d) \\ that\text{ is the same as} \\ a*d=b*c \end{gathered}`

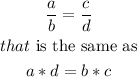
example option C

`\frac{3}{4\text{ }}<(4)/(5)`

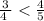
Multiply both sides by 4

`\begin{gathered} (3)/(4)*4<(4)/(5)*4 \\ 3<(16)/(5) \end{gathered}`

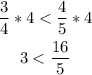
Now, multiply both sides by 5 (to remove the fraction of the right side)

`\begin{gathered} 3*5<(16)/(5)*5 \\ 15<16 \end{gathered}`

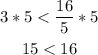
that is the same that multiplies in cross