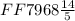Question

2 + 4/5 simplify form

Answer 1

Here we will deal with fractions and basic mathematical operations and simplify the result.

We are given the following algebraic expression for simplification as follows:

`2\text{ + }(4)/(5)`

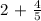
We will first go ahead and express both numbers in fractions for better understanding as follows:

`(2)/(1)\text{ + }(4)/(5)`

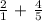
We see that their are two fractions with different numerical denominators. To perform the algebraic operation of addition we need the denominators to be equal.

To transform the denominators to an equivalent number we will find the LCM of the two denominators as follows:

`\begin{gathered} \text{LCM: 1 and 5} \\ \text{\textcolor{#FF7968}{LCM = 5}} \end{gathered}`

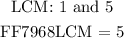
We see that the LCM of the denominators turns out to be 5. We will go ahead and multiply both the numerator and denominator of the first fraction so that the fraction actually remains unchanged as follows:

`\begin{gathered} (2)/(1)\cdot(5)/(5)\text{ + }(4)/(5) \\ \\ \textcolor{#FF7968}{(10)/(5)}\text{\textcolor{#FF7968}{ + }}\textcolor{#FF7968}{(4)/(5)} \end{gathered}`

Now we see that the denominators are equated. Now we can simply add the numerators and arrive at the result:

`\begin{gathered} (10+4)/(5) \\ \\ \textcolor{#FF7968}{(14)/(5)} \end{gathered}`

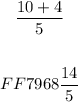
Now we will check whether the result can be simplified further or not. We see that numerator nor the denominator are multiples for one another. I.e 14 does not come in the table 5. Hence, there is no number with which we can divide both numerator or the denominator; hence, the simplfied result to the operation is as follows:

`\textcolor{#FF7968}{(14)/(5)}`