Question

Reasoning A cone with radius 3 and height 8 has its radius doubled. How many times greater isthe volume of the larger cone than the smaller cone? Use pencil and paper. Explain how thevolume of the cone would change if the radius were halved.The volume of the larger cone istimes greater than the volume of the smaller cone.

Answer 1

Let us firstly represent both cones as images:

To find the volume of a cone, we use the formula

`V=(1)/(3)\pi r^2h`

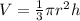
Volume of A

`\begin{gathered} V_A=(1)/(3)*\pi*3^2*8 \\ =24\pi \end{gathered}`

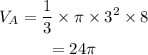
Volume of B

`\begin{gathered} V_B=(1)/(3)*\pi*6^2*8 \\ V_B=96\pi \end{gathered}`

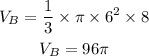
To find the number of times greater the larger cone is than the smaller cone, we will divide both volumes.

Hence,

`(V_B)/(V_A)`

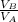
Substituting with the volumes above, we have

`\begin{gathered} (96\pi)/(24\pi) \\ =4 \end{gathered}`

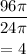
Therefore, we can see that the larger cone has 4 times greater volume than the smaller cone.