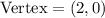From the question and graph provided we have a parabola (graph of a quadratic equation).
The characteristics of the graph includces amongst other things its "U" shape which clearly identifies a parabola.
ANSWER:
(a)
The parabola in this graph is an upside down "U" shaped graph which means it actually opens downwards.
(b)
The x-intercept(s) is defined as the point(s) where the parabola crosses the x-axis and at the same time the y-value is zero, that is,
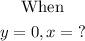
Along the horizontal line, y is always equal to zero, and at that point the graph touches the x-axis at x = 2. Therefore;

Similarly along the vertical line, x is always equal to zero, and at that point the graph touches the y-axis at y = -1. Therefore;
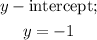
(c)
The vertex is the highest/lowest point on the parabola. That is the point where graph reaches its maximum and then begins to fall.
From the graph provided, the vertex here is at the point