Question

A retangler has a length at least four more than five times the width. If the perimeter is greater than or equal to 32 units, find the least possible with and length.

Answer 1

The perimeter of a rectangle is given by the formula

P=2(L+W)

In this problem

`L\ge5W+4\text{ ----> inequality 1}`
`P\ge32`

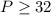
substitute given values

`2(L+W)\ge32`

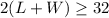
Solve for L

`\begin{gathered} L+W\ge(32)/(2) \\ \\ L+W\ge16 \\ L\ge16-W\text{ ---->inequality 2} \end{gathered}`

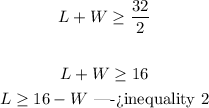
Equate both inequalities

`\begin{gathered} 5W+4=16-W \\ 5W+W=16-4 \\ 6W=12 \\ W=2 \end{gathered}`

Substitute the value of W in the inequality 1 or inequality 2

`\begin{gathered} L\ge5W+4 \\ L\geqslant5(2)+4 \\ L\geqslant14 \end{gathered}`

therefore

the least possible width and length are

L=14 units and W=2 units