Question

Find the sum of the first 6 terms of the following series, to the nearest integer. 15,5,5/3

Answer 1

S6 = 22

Explanation:

Given the series:

`15,5,(5)/(3)\cdots`

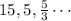
The sequence is a geometric sequence with:

• The first term, a = 15

,

• The common ratio, r = 1/3

The sum of nth terms of a geometric sequence is determined using the formula:

`S_n=(a(1-r^n))/(1-r)`

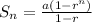
Substitute a=15, r=1/3 and n=6.

`\begin{gathered} S_6=(15(1-((1)/(3))^6))/(1-(1)/(3)) \\ =(15(1-(1)/(729)))/((2)/(3)) \\ =(15((728)/(729)))/((2)/(3)) \\ =(1820)/(81) \\ =22.47 \\ \implies S_6\approx22 \end{gathered}`

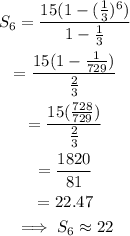
The sum of the first 6 ters of the series is 22. (roundd to the nearest integer)