Question

A complex rational expression is a rational expression in which the numerator or denominator contains a rational expression. Provide three (3) examples.

Answer 1

A rational expression is a fraction in which the numerator and denominator are polynomials and a complex rational expression is a fraction where the numerator and denominator are rational expressions.

For example, we can take the following rational expressions:

`\begin{gathered} f(x)=(x^2-9x+5)/(x+1) \\ g(x)=(x^3+2x)/(2x^2+8) \end{gathered}`

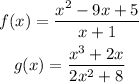
Both f(x) and g(x) are polynomial functions, we can use f(x) as the numerator of a complex rational expression and g(x) as the denominator to get:

`((x^2-9x+5)/(x+1))/((x^3+2x)/(2x^2+8))`

Similarly, we can formulate 2 more complex rational expressions like this:

`\begin{gathered} \frac{\frac{x^2^{}+3}{x^3+2x-1}}{(2x-4x^2)/(x)} \\ \\ ((3)/(x-3))/((4x+4)/(2)) \end{gathered}`