Question

I ALSO NEED THE SOLUTION where do I place it

Answer 1

Given the System of Inequalities:

`\begin{cases}y\leq-3x+1 \\ \\ y>(2)/(3)x-2\end{cases}`

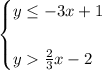
You can identify that the boundary lines are:

`\begin{gathered} y=-3x+1 \\ \\ y=(2)/(3)x-2 \end{gathered}`

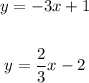
By definition, the Slope-Intercept Form of the equation of a line is:

`y=mx+b`

Where "m" is the slope of the line and "b" is the y-intercept.

In this case, you can identify that the y-intercept of the first line is:

`b_1=1`

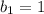
And the y-intercept of the second line is:

`b_2=-2`

In order to find the x-intercept, you can substitute this value of "y" into each equation and solve for "x" (because the value of "y" is zero when the line intersects the x-axis):

`y=0`

Then, for the first line, you get:

`\begin{gathered} 0=-3x+1 \\ \\ -1=-3x \\ \\ (-1)/(-3)=x \\ \\ x=(1)/(3) \\ \\ x=0.333 \end{gathered}`

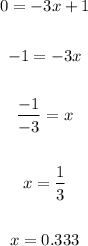
And for the second line:

`\begin{gathered} 0=(2)/(3)x-2 \\ \\ 2=(2)/(3)x \\ \\ (2)(3)=2x \\ \\ (6)/(2)=x \\ \\ x=3 \end{gathered}`

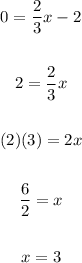
Now you know that the first line passes through these points:

`\mleft(0.333,0\mright),\mleft(0,1\mright)`

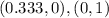
And the second line passes through these points:

`(3,0),(0,-2)`

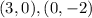
Notice that the symbol of the first inequality is:

`\leq`

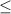
That indicates the boundary line is solid and the shaded region is below the line.

The symbol of the second inequality is:

`>`

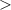
It indicates that is the boundary line is dashed and the shaded region is above the line.

The solution region is the intersection region between the inequalities.

Knowing the above, you can graph the System of inequalities.

Hence, the answer is: