PartA
The probability of picking an even number or a multiple of three is a theoretical probability because the sample space(the possible outcome) can easily be gotten and hence the probability of the event can be calculated using the formula
Part B
Let the probability of picking an even number =P(A)
probability of picking a multiple of three =P(B)
hence using theoretical probability
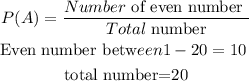
Hence
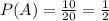
Multiples of 3 between 1-20 are 3, 6,9,12,15,18=6
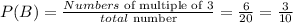
Then, the probability of P(A) or P(B) is the addition of the individual probability
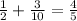
Therefore the probability of picking an even number or a multiple of three is 0.8