To find the measure of every interior angle of a regular hexagon, first, we need to find the sum of the internal angles of a hexagon.
1. To find that, we need to use the following formula:
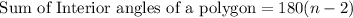
Where n is the number of sides of a polygon. Since a hexagon has 6 sides, then n = 6, and we have:

Then the sum of the interior angles of a hexagon is 720 degrees.
2. Now, to find the measure of each interior angle of a regular hexagon, we need to apply the next formula:
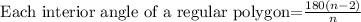
And then, for n = 6 (regular hexagon), we have:
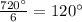
Therefore, in summary, the measure of every interior angle of a regular hexagon is 120° (120 degrees).