Question

Solve the system of equations below using elimination write your answer in form (x,y) -4X - 2Y = -124x + 8y = -24

Answer 1

The system of equations given is a pair of linear equations.

To solve the system of equations, we solve them simultaneously using the elimination method.

To use the elimination method, one of the unknowns must be cancelled out from the equations.

To do this, the magnitude of the coefficient of the unknown to be cancelled out must be the same.

Given:

`\begin{gathered} -4x-2y=-12\ldots\ldots\ldots\ldots\ldots\text{.}\mathrm{}(1) \\ 4x+8y=-24\ldots\ldots\ldots\ldots\ldots\ldots.(2) \end{gathered}`

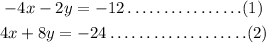
From the above equations, the coefficient of x is 4 and -4 in both equations.

Hence, we can eliminate x by adding the two equations.

Equation (1) + (2) gives;

`\begin{gathered} -4x+4x-2y+8y=-12+(-24) \\ 0+6y=-12-24 \\ 6y=-36 \\ \text{Dividing both sides by 6 to g}et\text{ the value of y,} \\ y=-(36)/(6) \\ y=-6 \end{gathered}`

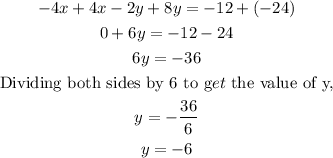
To solve for x, we substitute the value of y gotten in any of the two equations.

Substituting y in equation (1);

`\begin{gathered} -4x-2y=-12 \\ -4x-2(-6)=-12 \\ -4x+12=-12 \\ -4x=-12-12 \\ -4x=-24 \\ \text{Dividing both sides by -4 to get the value of x;} \\ x=(-24)/(-4) \\ x=6 \end{gathered}`

Therefore, the solution to the system of equations in the form (x,y) is (6,-6)