Given data:
The first given side is FG=21.
The second given side is GH=12.
The expression for the Pythagoras theorem is,
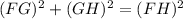
Substitute the given values in the above expression.
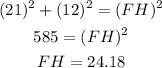
The expression for the angle F is,
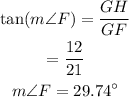
The angle H is,
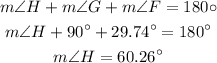
Thus, the FH length is 24.18, m∠F=29.74 degrees, and m∠H is 60.26 degrees.