Answer:
y=2x+6
Step-by-step explanation:
Given any two points on a line, to find the equation of the line, we can use the two-point form of the equation of a line stated below.
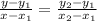
If the points are:
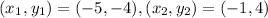
Substitute into the formula:
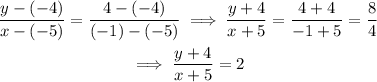
Next, we write it in the slope-intercept form:
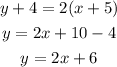
The equation of the line is y=2x+6.