Question

Solve the equation using a table. x^2-14x+48=0

Answer 1

The solution of the equation is (8, 6)

Explanation:

The quadratic equation is given below as

`x^2\text{ - 14x + 48 = 0}`

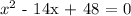
Recall that, the standard form of the quadratic function is given as

`ax^2\text{ + bx + c = 0}`

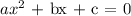
Relating the two together, we have the following data

• a = 1

,

• b = -14

,

• c = 48

The next thing is to find ac

`\begin{gathered} a\text{ = 1 and c = 48} \\ ac\text{ = 1 x 48} \\ ac\text{ = 48} \end{gathered}`

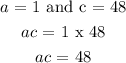
Factors of 48: 1 and 48, 2 and 24, 4 and 12, 6 and 8, -1 and -48, -2 and -24, -4 and -12, -6 and -8

The next step is to find the factors of 48 that will give -14 when add and 48 when multiply together

The factors are -6 and -8

`\begin{gathered} x^2\text{ -6x - 8x + 48 = 0} \\ x(x\text{ - 6) - 8(x - 6) = 0} \\ (x\text{ - 6) (x - 8) = 0} \\ (x\text{ - 6) = 0 or (x - 8) =0} \\ x\text{ - 6 = 0 or x - 8 = 0} \\ x\text{ = 0 + 6 or x = 0 + 8} \\ x\text{ = 6 or x = 8} \end{gathered}`

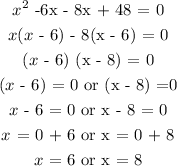
Hence, the solution of the equation is x = 6 or x = 8