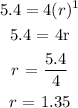We have the general form as;
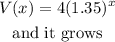
Here, we want to select the correct option that models the data in the table
Generally, for an exponential equation, the general form is given as;
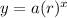
Where y is the value after some time x
a represents the initial value
r represents the rate of change
x is the time frame
Looking at the question, we can see that as the value of x is increasing (time) ; the value of v(x) is increasing. So what this mean is thet v(x) is increasing over time and hence, what we have is a growth.
Now, when x is 0, we have a value of v(x); that means the initial value is 4
So lastly, we need to get the rate of change r;
we can get it by substituting;
We have this as;