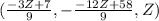Question

3. Solve the system using elimination (not substitution or matrices). negative 2 x plus y minus 2 z equals negative 8A N D7 x plus y plus z equals negative 1A N D5 x plus 2 y minus z equals negative 91. If the system has a single solution, write the solution as an ordered triple, (x, y, z).2. If the system has infinite solutions, write the solutions IN TERMS OF z.The solution should look something like left parenthesis 3 minus 3 z comma space minus 1 plus 7 z comma space z right parenthesis but not like left parenthesis negative 6 plus 3 y comma space y comma space 2 minus 5 y right parenthesis or not like left parenthesis x comma space 3 plus 5 x comma space minus 1 plus 4 x right parenthesis. None of these are the solution, they are just examples of what the answer could look like and not look like.

Answer 1

Elimination Method

`\begin{gathered} -2X+Y-2Z=-8 \\ 7X+Y+Z=-1 \\ 5X+2Y-Z=-9 \end{gathered}`

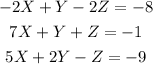
If we multiply the equation 3 by (-1) we obtain this:

`\begin{gathered} -2X+Y-2Z=-8 \\ 7X+Y+Z=-1 \\ -5X-2Y+Z=9 \end{gathered}`

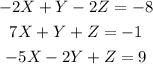
If we add them we obtain 0, therefore there are infinite solutions. So, let's write it in terms of Z

1. Using the 3rd equation we can obtain X(Y,Z)

`\begin{gathered} 5X=-9-2Y+Z \\ X=(-9-2Y+Z)/(5) \\ \end{gathered}`

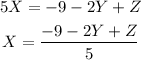
2. We can replace this value of X in the 1st and 2nd equations

`\begin{gathered} -2\cdot((-9-2Y+Z)/(5))+Y-2Z=-8 \\ 7\cdot((-9-2Y+Z)/(5))+Y+Z=-1 \end{gathered}`

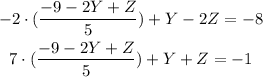
3. If we simplify:

`\begin{gathered} (-9Y+12Z-63)/(5)=-1 \\ (9Y-12Z+18)/(5)=-8 \end{gathered}`

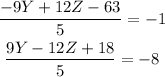
4. We can obtain Y from this two equations:

`\begin{gathered} Y=-(-12Z+58)/(9) \\ \end{gathered}`

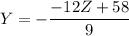
5. Now, we need to obtain X(Z). We can replace Y in X(Y,Z)

`\begin{gathered} X=(-9-2Y+Z)/(5) \\ X=(-9-2(-(-12Z+58)/(9))+Z)/(5) \end{gathered}`

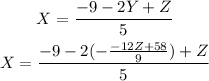
6. If we simplify, we obtain:

`X=(-3Z+7)/(9)`

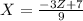
7. In conclusion, we obtain that

(X,Y,Z) =

`((-3Z+7)/(9),-(-12Z+58)/(9),Z)`