Question

What is the range of the function y=|x+2| -2 if the domain is x e R

Answer 1

Given the function;

`y=|x+2|-2`

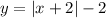
The range of the function can be derived by finding the lowest and highest possible value of the function.

For the function, the lowest value is at;

`|x+2|=0`

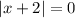
Since |x+2| cannot be less than zero.

So, The lowest value of y is;

`\begin{gathered} y=|x+2|-2 \\ y=0-2 \\ y=-2 \end{gathered}`

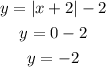
The highest value is infinity, because the higher the value of |x+2| the higher the value of the function.

Therefore, the range of the function is;

`y\ge-2`

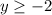
Because the lowest possible value is -2 and the highest possible value is infinity.