Question

Given the unit circle what is the value of x

Answer 1

Given the figure, we can deduce the following information:

1. The two given points are:

(1,0)

(x,-7/10)

To determine the value of x, we must note first that the x value on the first quadrant is 1 so the radius of the circle must be equal to 1.

Next, we apply the equation for unit circle:

`x^2+y^2=1`

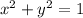
Then, we plug in y=-7/10 into x^2+y^2=1:

`\begin{gathered} x^2+y^2=1 \\ x^2+(-(7)/(10))^2=1 \\ x^2+(49)/(100)=1 \\ \text{Simplify and rearrange} \\ x^2=1-(49)/(100) \\ x^2=(51)/(100) \\ x=\pm\sqrt[]{(51)/(100)} \\ x=\pm\frac{\sqrt[]{51}}{10} \end{gathered}`

But since the point is in the third quadrant, the value of x must be negative. Therefore, the answer is:

`x=-\frac{\sqrt[]{51}}{10}`