Step-by-step explanation:
For compound interest, we have the following equation

Where A is the amount after t years, P is the initial amount, r is the interest rate and n is the number of times the interest is compound.
In this case, we know
A = $2500
P = $1000
r = 7% = 0.07
n = 12 (compounded monthly)
t = ?
So, replacing the values, we get:
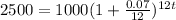
Now, we need to solve for t

Therefore, it needs 13.13 years to produce $2500