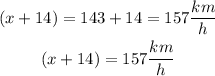Question

two trains leave towns 1800 kilometers apart at the same time and travel toward each other. onr train leaves 14 km/h slower than the other. if they meet in 6 hours, what is the rate of each train?

Answer 1

Let xkm/h represent the speed of the slower train

Since the faster train is 14km/h faster than the slower train, the speed of the faster train is (x+14)km/h

Since they meet after 6 hours, then it is the time taken to cover the distance 1800km

The formula for speed is

`\text{Speed}=\frac{\text{Distance}}{\text{Time}}`

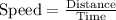
The distance travel by the slower train will be

`\begin{gathered} \text{Speed}=\frac{\text{Distance}}{\text{Time}} \\ x=\frac{\text{Distance}}{6} \\ \text{Crossmultiply} \\ \text{Distance}=x*6=6xkm \end{gathered}`

The distance traveled by the slower train is 6xkm

The distance traveled by the faster train will be

`\begin{gathered} \text{Speed}=\frac{\text{Distance}}{\text{Time}} \\ (x+14)=\frac{\text{Distance}}{6} \\ \text{Distance}=(x+14)*6 \\ \text{Distance}=6(x+14)km_{} \end{gathered}`

The distance traveled by the faster train is 6(x+14)km

The total distance will be

`6x+6(x+14)=1800`

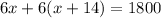
Solve to find x

Since, xkm/h is the speed of the slower train,

Hence, the rate of the slower train is

`x=143(km)/(h)`

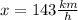
Since, (x+14)km/h is the speed of the faster train,

Hence, the rate of the faster train is

`\begin{gathered} (x+14)=143+14=157(km)/(h) \\ (x+14)=157(km)/(h) \end{gathered}`