Question

A table of values of a linear function is shown below

Answer 1

Part A: Solving for the slope.

Recall that given two points in the line, the slope of a linear function is given by the equation

`\begin{gathered} m = (y_2 - y_1)/(x_2 - x_1) \\ \text{where} \\ (x_1,y_1)\text{ and }(x_2,y_2)\text{ are the two points.} \end{gathered}`

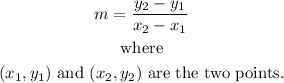
In this instance we will be using points (0,-4) and (1,-5).

Substitute these two points and we get

`\begin{gathered} (x_1,y_1)=(0,-4) \\ (x_2,y_2)=(1,-5) \\ \\ m = (y_2 - y_1)/(x_2 - x_1) \\ m=(-5-(-4))/(1-0) \\ m=(-5+4)/(1) \\ m=(-1)/(1) \\ m=-1 \end{gathered}`

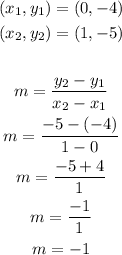
Therefore, the slope of the linear function is -1.

Part B: Solving for y-intercept

The y-intercept is the value of y, when x = 0.

In the given table, when x = 0, y = -4. Therefore, the y-intercept of the linear function is -4.

Part C: Equation of the line

The slope-intercept form of a line equation is in the form

`\begin{gathered} y=mx+b \\ \text{where} \\ m\text{ is the slope} \\ b\text{ is the y-intercept} \end{gathered}`

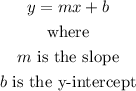
As solved earlier, the slope is -1, and the y-intercept is -4.

Substitute m = -1, and b = -4, to the slope-intercept form. The equation of the line therefore is

`\begin{gathered} y=mx+b \\ y=(-1)x+(-4) \\ \\ \text{Simplify and we get} \\ y=-x-4\text{ \lparen final answer\rparen} \end{gathered}`