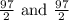Step-by-step explanation
From the statement, we must find the dimensions of a rectangle with:
• perimeter P = 194,
,
• the largest area.
We consider a rectangle with sides x and y. We will write formulas for P (the perimeter) and A (the area). Then we will express the area in terms of one side A(x), and maximize the function.
(1) The perimeter of the rectangle is:
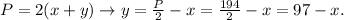
(2) The area of the rectangle is:
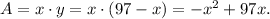
(3) To maximize the area A(x), we compute and make equal to zero its first derivative, then we solve for x:

(4) From point (1), we find the length of the other side:
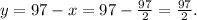
Answer
The dimensions of the rectangle with a perimeter of 194 and the largest area are: