Two lines are parallel if they have the same slope
Given two points (x1, y1) and (x2, y2) of the line, its slope (m) is computed as follows:
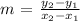
From the picture, points (0,-2) and (2, -3) lie on the line. Then, its slope is:
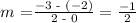
Then, the first and fifth options are parallel to the line in the picture.
From the case: 2y = -x - 4, we have to isolate y, as follows:
y = (-x - 4)/2
y = -1/2 x - 4/2
y = -1/2 x - 2
Therefore, this line is parallel too.
From the case: x + 2y = 8, we have to isolate y, as follows:
2y = 8 - x
y = (8 - x)/2
y = 8/2 - 1/2 x
y = 4 - 1/2 x
Therefore, this line is parallel too.