I need help finding the circumference of a circle on question 4 and 6

Question

asked May 20, 2023 46.1k views

1 Answer

Knub · Answer 1 · 2023-05-23T18:20:23+0000

Given:

4. Diameter of the circle, d = 58 yd.

6. Diameter of the circle, d = 10.2 m

Required:

We need to find the circumference of a circle.

Step-by-step explanation:

4.

Consider the formula to find the radius.

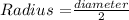
$Radius\text{ =}(diameter)/(2)$

Substitute diameter = 58 in thr formula.

$Radius\text{ =}(58)/(2)=29yd$

Consider the formula to find the circumference of a circle.

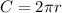
$C=2\pi r$

Substitute r =29 in the formula.

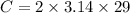
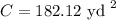
$C=182.12\text{ yd }^2$

Answer:

The circumference of a circle is 182.12 square yards.

6)

Consider the formula to find the radius.

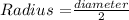
$Radius\text{ =}(diameter)/(2)$

Substitute diameter = 10.2 in thr formula.

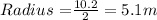
$Radius\text{ =}(10.2)/(2)=5.1m$

Consider the formula to find the circumference of a circle.

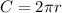
$C=2\pi r$

Substitute r =5.1m in the formula.

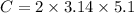
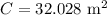
$C=32.028\text{ m}^2$
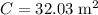
$C=32.03\text{ m}^2$

Answer:

The circumference of a circle is 32.03 square meters.