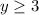We have the following function given:
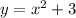
The domain is all the possible values for x in the function and as we can see we don't have any restriction so then the domain would be all the reals.
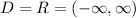
And for the range we need to take in count that we have a parabola open upward so then the minimum value would be the vertex given by:
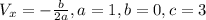
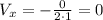
And the y minimum value would be:
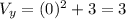
Then the range would be given by:
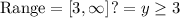
Final answer: