Consider the given function,
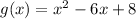
Apply the quadratic formula to find the roots,
![\begin{gathered} x=\frac{-(-6)\pm\sqrt[]{(-6)^2-4(1)(8)}}{2(1)} \\ x=\frac{6\pm\sqrt[]{36-32}}{2} \\ x=\frac{6\pm\sqrt[]{4}}{2} \\ x=(6\pm2)/(2) \\ x=2,4 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/qopaadu3slevb68rw7sbulteop3vozde5q.png)
Consider the following,
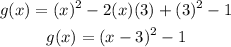
This is the vertex form of the quadratic equation. And the vertex of the parabola is (3,1).
Consider that the axis of symmetry of a quadratic equation is calculated as,
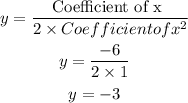
Thus, the axis of symmetry is the vertical line y=-3.
There are various conclusions which you can make comparing the function g(x) and f(x). Note that the function f(x) has both roots equal to zero, while g(x) has roots 2 and 4.
So we can conclude that the function f(x) is tangent to the x-axis at the origin, while the function g(x) intersects the x-axis twice.