Question

Identify the lines that are perpendicular: A. = −5 and = 2 are perpendicularB. + 5 = 2 and − 5 + = 3 are perpendicularC. = 13 + 1 and − 1 = −3( − 5) are perpendicularD. − 5 = + 1 and + = 3 are perpendicularE. + 2 = 13 ( − 6) and = 3 + 4 are perpendicular

Answer 1

In order to check if the lines are perpendicular, we need to check if their slopes have the following relation (to find the slope we can use the slope-intercept form y = mx + b):

`m_1=-(1)/(m_2)`

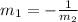
A.

In this option, y = -5 is an horizontal line and x = 2 is a vertical line, therefore they are perpendicular.

B.

First let's find the slope of each line:

`\begin{gathered} x+(y)/(5)=2 \\ 5x+y=10 \\ y=-5x+10\to m=-5 \\ \\ -(x)/(5)+y=3 \\ y=(x)/(5)+3\to m=(1)/(5) \end{gathered}`

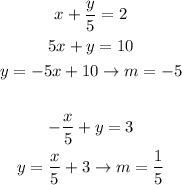
These slopes obey the relation stated above, so the lines are perpendicular.

C.

`\begin{gathered} y=(1)/(3)x+1\to m=(1)/(3) \\ \\ y-1=-3(x-5) \\ y-1=-3x+15 \\ y=-3x+16\to m=-3 \end{gathered}`

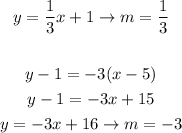
These slopes obey the relation stated above, so the lines are perpendicular.

D.

`\begin{gathered} y-5=x+1 \\ y=x+6\to m=1 \\ \\ x+y=3 \\ y=-x+3\to m=-1 \end{gathered}`

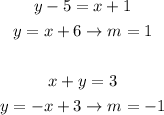
These slopes obey the relation stated above, so the lines are perpendicular.

E.

`\begin{gathered} y+2=(1)/(3)(x-6) \\ y+2=(1)/(3)x-2 \\ y=(1)/(3)x-4\to m=(1)/(3) \\ \\ y=3x+4\to m=3 \end{gathered}`

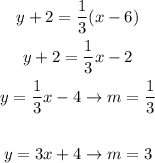
These slopes don't obey the relation stated above, so the lines aren't perpendicular.

The correct options are A, B, C and D.