Question

Draw one card from a standard deck. Find P(ace)

Answer 1

Concept

A standard deck of playing cards contains 52 cards. Divided equally into two colors "Red" and "Black". Deck of 52 cards has four suits "Spades", "Hearts", "Diamonds" and "Clubs". ... Each 4 suits contains 13 cards : Ace, 2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, Queen, King.

The total number of cards in a pack of a card is 52

Total number of Aces = 4

Use thr formula below to find the probability of drawing one card from a standard deck that is ace.

Probability of any event

`=\text{ }\frac{N\text{umber of required outcomes}}{N\text{umber of total possible outcomes}}`

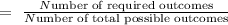
Number of total possible outcomes is the total number of cards in a deck of card.

= 52

Number of required outcomes is the number of ace cards in a deck of card

= 4

Probability of drawing an ace card

`\begin{gathered} =\text{ }(4)/(52) \\ =\text{ 0.077} \\ =\text{ 0.077 x 100\%} \\ =\text{ 7.7\%} \end{gathered}`

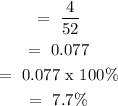
Final answer in percentage = 7.7%