Hello there. To solve this question, we'll have to remember some properties about determining tangent of angles using the unit circle.
First, remember the unit circle:
Say we have a segment going from the origin to a point of the circle, forming an angle theta with the x axis, as follows
To define the tangent of this angle, we in fact draw a tangent line to this unit circle at (1, 0) (or theta = 0).
The tangent is defined as the measure in the blue line below (or above, in case theta is from the second and fourth quadrants) the intercept.
The point in the circle will have coordinates:
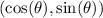
With this, we can solve this question.
Remember that in the unit circle, a 180º angle represents the point (-1, 0), that is:
So that the tangent line will be given by the above yellow line.
If you extend the segment leaving from the point going through the origin and intercepting the tangent line, you'll get.
So, according the definition we had above, the tangent of this angle should be the measure of the segment determined by the interception, but as you can see the interception is at the origin.
This means that the tangent of this angle is 0.
In fact, for every multiple of pi/2, the tangent function has an asymptote and has roots for every multiple of pi.