Question

What is the rate I wish the oil is flowing?

Answer 1

Given:

• Diameter of pipe = 0.753 m

,

• Diameter of constricted section = 0.4518 m

,

• Density of oil = 821 kg/m³

,

• Presure in pipe = 9100 N/m²

,

• Pressure in constricted section = 6825 N/m²

Let's find the rate at which the oil is flowing.

Here, we are to apply Bernoulli's equation.

We have:

`\begin{gathered} A_1* v_1=A_2* v_2 \\ \\ p_1+0.5pv^2_1=p_2+0.5pv^2_2 \end{gathered}`

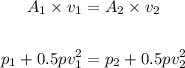
Thus, we have:

`(v_2)/(v_1)=((d_2)/(d_1))^2=((0.753)/(0.4518))^2=2.78_{}^{}`

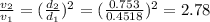
Using the equation, we have:

`\begin{gathered} 9100+0.5(821)v^2_1=6825+0.5(2.78)^2v^2_1*821 \\ \\ 9100+410.5v^2_1=6825+3169.06v^2_1 \\ \\ 3169.06v^2_1-410.5v^2_1=9100-6825 \\ \\ 2758.56v^2_1=2275 \\ \\ v^2_1=(2275)/(2758.56) \end{gathered}`

Solving further:

`\begin{gathered} v^2_1=0.8247 \\ \\ v_1=\sqrt[]{0.8247} \\ \\ v_1=0.908\text{ m/s} \end{gathered}`

Thus, we have:

`\begin{gathered} 0.25\pi*(0.753)^2*(0.908) \\ \\ =0.404536m^3\text{ /s} \end{gathered}`

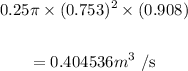
Therefore, the rate at which the oil flowing is 0.404536 m^3/s.

ANSWER:

0.404536 m³/s.