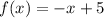Step 1. We label the points to Find the slope of the line.
The points we have are (4,1) and (2,3), we label them as follows:
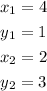
Step 2. Use the slope formula to find the slope "m":

Substituting our values:
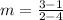
Solving the operations:
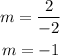
Step 3. Now that we have the slope, we use the point-slope equation to find the equation of the line.
The point-slope equation is:

Substituting the values of m, x1, and y1:
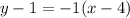
now we solve this equation for y by using the distributive property on the right side of the equation:
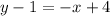
Add 1 to both sides:

Step 4. Change to function notation.
To do this, we change "y" for "f(x)":
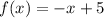
Answer: