Question

Greg invested 5500 in an account that pays an annual rate 2.3%, compounded daily. Assume there are 365 days in each year. Answer each part.

Answer 1

It is given that the amount invested is $5500, the annual rate is 2.3% which is compounded daily (365 times in a year).

(a) Recall that the Amount in an account whose interest is compounded is given as:

`A=P\left(1+(r)/(n)\right)^(nt)`

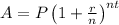
Where P is the amount invested, r is the annual rate, n is the number of times it is compounded in a year, and t is the number of years.

Substitute P=5500, r=2.3%, t=1, and n=365 into the formula:

`A=5500\left(1+(2.3\%)/(365)\right)^(365(1))\approx\$5627.96`

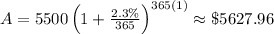
(b) The effective annual interest rate, R is given as:

`R=\left(1+(r)/(n)\right)^n-1`

Substitute r=2.3% and n=365 into the formula:

`R=\left(1+(2.3\%)/(365)\right)^(365)-1\approx0.023226\approx2.32\%`

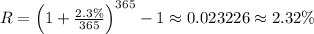
Answers:

(a) $5627.96

(b) 2.32%