Question

A student created this table to represent a linear relationship between x and y.X Y-2. 10.0-1. 7.50. 5.01. 2.52. 0The student says the point (9,-17.5) lies on the line represented by the relationship between x and y shown in the table.Is the student correct? Show or explain how you got your answer.

Answer 1

The relationship between x and y is represent as:

Since, the relationship is linear.

The standard form of equation of line is:

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

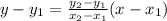
Consider any two set x and y values from the given relationship.

Let (-2, 10) and (-1,7.5)

`\text{Substitute x}_1=-2,y_1=10,x_2=-1,y_2=7.5\text{ in the standard equation of line.}`

`\begin{gathered} y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1) \\ y-10=(7.5-10)/(-1-(-2))(x-(-2)) \\ y-10=(-2.5)/(1)(x+2) \\ y-10=-2.5(x+2) \\ y=-2.5(x+2)+10 \end{gathered}`

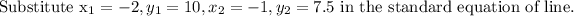
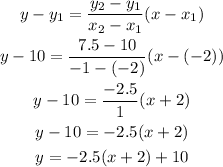
The equation of the linear relationship between x and y is:

y = -2.5(x + 2) + 10

Now, to check that the point (9, -17.5) lies on the represented relationship between x and y

Substitute x = 9 and y = -17.5 in the equation y = -2.5(x + 2) + 10

y = -2.5(x + 2) + 10

-17.5 = -2.5(9 + 2) + 10

-17.5 = -2.5(11) + 10

-17.5 = -27.5 + 10

-17.5 = -17.5

Thus, LHS = RHS

Hence the point (9, -17.5) lie on the given linear relationship between x and y.

Answer: The point (9, -17.5) lie on the given linear relationship between x and y.