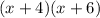Question

y = (x - 4)(x + 2) + :: y = (x - 6)(x - 3) · y = (x + 6)(x + 3) y=-(+ 3) (x - 1) :: y = - (x - 3)(x + 1) :: y = (x + 6)(x + 4) 1 2 3 4 5 6 7

Answer 1

Looking at the first graph, the roots (that is, the points where the graph intersects the x-axis) are x = -6 and x = -4.

So, we can write the equation in the following form:

`a(x-x_1)(x-x_2)_{}`

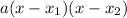
Where x1 and x2 are the roots. So for the first graph we have:

`\begin{gathered} (x-(-6))\cdot(x-(-4)) \\ =(x+6)(x+4) \end{gathered}`

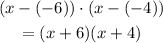
Now, for the second graph, the roots are -2 and 4, so the equation is:

`\begin{gathered} (x-(-2))\cdot(x-4) \\ =(x-4)(x+2) \end{gathered}`

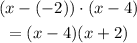
For the third graph, the roots are -6 and -3 and the concavity is downwards (so a = -1), so the equation is:

`-(x+3)(x+6)`

For the fourth graph, the roots are -3 and 1 and the concavity is downwards, so the equation is:

`-(x-1)(x+3)`

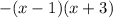
For the fifth graph, the roots are -6 and -4, so the equation is:

`(x+4)(x+6)_{}_{}_{}`