Question

Find the coordinates of B,C and D given that AB=5 and BC=10

Answer 1

Given that AB = 5, then:

`x_B-x_A=5`

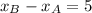
where xB and xA are the x-coordinates of A and B. Replacing with xA = -2,

`\begin{gathered} x_B-(-2)=5 \\ x_B+2=5 \\ x_B=5-2 \\ x_B=3 \end{gathered}`

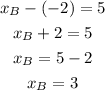
From the picture, the y-coordinate of B is the same as A. Then point B is located at (3, -5)

Given that BC = 10, then:

`y_C-y_B=10`

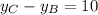
where yB and yC are the Y-coordinates of B and A. Replacing with yB = -5,

`\begin{gathered} y_C-(-5)=10 \\ y_C+5=10 \\ y_C=10-5 \\ y_C=5 \end{gathered}`

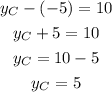
From the picture, the x-coordinate of B is the same as C. Then point C is located at (3, 5)

The slope of the line that passes through points A and C is:

`\begin{gathered} m=(y_C-y_A)/(x_C-x_A) \\ m=\frac{5_{}-(-5)_{}}{3_{}-(-2)} \\ m=(10)/(5) \\ m=2 \end{gathered}`

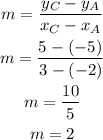
Given that the line passes through (-2, -5), then its y-intercept is:

y = mx + b

-5 = 2(-2) + b

-5 = -4 + b

-5 + 4 = b

-1 = b

Point D coincides with this y-intercept, then point D is located at (0, -1)